Exercise 1.6 from Stein and Shakarchi's Fourier Analysis

Exercise 1.6 from Stein and Shakarchi’s Fourier Analysis

The problem is as follows:

We have

$\begin{align*}g'(t) &= f'(t) \cos ct - c f(t) \sin ct - c^{-1} f''(t) \sin ct - f'(t) \cos ct \\&= - c f(t) \sin ct - c^{-1} f''(t) \sin ct \\&= - \frac{1}{c} \left( \sin ct) (f''(t) + c^2 f(t) \right) \\&= 0\end{align*}$

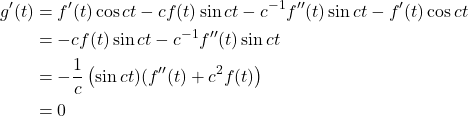
and

$\begin{align*}h'(t) &= f'(t) \sin ct + c f(t) \cos ct + c^{-1} f''(t) \cos ct - f'(t) \sin ct \\&= c f(t) \cos ct + c^{-1} f''(t) \cos ct \\&= \frac{1}{c} \left( \cos ct) (f''(t) + c^2 f(t) \right) \\&= 0.\end{align*}$

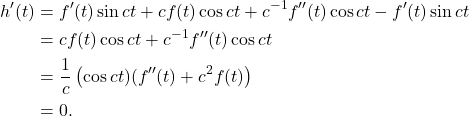
Each equality with $0$ follows from the assumption $f''(t) + c^2 f(t) = 0$ . Therefore $g'(t) = h'(t) = 0$ and $g(t), h(t)$ are constant.

The problem asks for constants $a$ and $b$ . Could it be that $g(t)$ and $h(t)$ are these constants? That would be a natural guess. Let’s just try computing the sum